跳至内容
 莱昂哈德·欧拉(Leonhard Euler)是数学史上最多产的一位数学家。他生前共出版了 800 多篇论文和著作,其中 58% 是数学方面的,物理-力学和天文学各占了 28%和 11%,余下 3% 是关于航海学和建筑学[1]。不可思议的是,即便在他逝世后,人们又整理发现了他的 400 多篇尚未发布的论文。时至今日,其著作和信件仍未全部面世——它们多达70卷,长达几万页。
莱昂哈德·欧拉(Leonhard Euler)是数学史上最多产的一位数学家。他生前共出版了 800 多篇论文和著作,其中 58% 是数学方面的,物理-力学和天文学各占了 28%和 11%,余下 3% 是关于航海学和建筑学[1]。不可思议的是,即便在他逝世后,人们又整理发现了他的 400 多篇尚未发布的论文。时至今日,其著作和信件仍未全部面世——它们多达70卷,长达几万页。
[1] 蔡天新, 《难以企及的人物 – 数学天空的群星闪耀》
欧拉涉足的研究领域十分广泛,从数论、圆几何、音乐理论等“纯粹”研究,到无穷级数、对数、微积分和力学,再到光学、天文学、行星运动、航海学及其它实用领域。欧拉提出的想法如此之多,以至于其后继者们一直忙于跟进这些想法。法国应用数学家皮埃尔-西蒙·拉普拉斯(Pierre-Simon Laplace)对人们提出了这样的忠告:“读读欧拉吧,他是我们所有人的老师。”
许多概念无疑都以欧拉的名字命名:欧拉常数、多面体欧拉定理、三角形的欧拉线、欧拉动力学方程、欧拉图、欧拉五边形数定理等等。
欧拉的一生可以分为四个时期。1707年4月15日,生于瑞士巴塞尔,在那里长大并步入大学。20岁时,在俄罗斯圣彼得堡学院担任数学系教授。然而由于在圣彼得堡的处境愈发艰难,于1741年移居柏林,并在那里生活了25年。而再次由于处境艰难(虽原因不同),于1766 年回到圣彼得堡,在那里度过了余生,最终于1783年去世。
▌巴塞尔时期
欧拉的父亲保罗·欧拉(Paul Euler)是一名谦逊的基督教加尔文宗的牧师,他希望子承父业。于是小欧拉在14岁时进入巴塞尔大学(这个入学年龄在当时看来并不奇怪),主修神学、希伯来语、法学和哲学。
但在大学期间,欧拉遇到了当时欧洲最优秀的数学家约翰·伯努利(Johann Bernoulli)。他对欧拉的数学能力印象深刻,同意在每周六为他单独授课,并很快意识到他的这位学生是多么与众不同。欧拉也与他的两个儿子丹尼尔·伯努利(Daniel Bernoulli)和尼古拉二世·伯努利(Nicolaus II Bernoulli)成为挚友,尽管尼古拉不久后便去世了。
1724年,17岁的欧拉取得了哲学硕士学位之后,受到父亲的影响便进入神学院为一名合格的牧师做准备。
“我必须进入神学系读书,并认真学习希腊语和希伯来语,但我并没有取得多少进展,因为我将大部分的时间都用在了学习数学。且令我开心和幸运的是,我每周六仍可以去拜访约翰·伯努利先生。”
幸运的是,虽然欧拉的父亲十分不情愿,但伯努利还是说服他相信自己那位天赋异禀的儿子是命中注定要成为一名伟大的数学家。于是,欧拉被允许离开神学系,开始了他璀璨耀眼的数学生涯。
欧拉在 20 岁时就取得了第一个重要的数学成就。他在回忆录中写道,巴黎科学院曾主办过一个有奖征文竞赛,问题是如何找出船上桅杆的最优放置。欧拉的论文落败在当时“舰船建造学之父”的皮埃尔·布格之手,只获得二等奖。不过,欧拉此后共获一等奖了 12 次之多!
之后,欧拉试图留在巴塞尔大学申请数学系教授一职,遗憾没能成功。此时,好友丹尼尔·伯努利正在俄罗斯圣彼得堡科学院任职,并邀请欧拉前来。但当时职位紧缺,唯有医学和生理学系的教职仍有空席,因此,欧拉就自学了这些科目,并在对耳部研究的过程中对声音的数学原理和波的传播产生了兴趣。
▌前圣彼得堡的时期
就在1727年5月17日欧拉抵达俄罗斯的当天,命运给他开了个玩笑。俄国开明的女皇叶卡捷琳娜一世在这天就去世了,同时俄国皇家科学院也就失去了当权者的支持。
▲ 腓特烈大帝、 叶卡捷琳娜二世、叶卡捷琳娜一世画像
当时,皇位的继承者彼得二世还是个小男孩,由俄国贵族掌权的派系将科学院看作是一种不必要的财政负担,不仅切断了很多科研资助,而且还经常找外籍人员的麻烦。
欧拉只埋头于自己的研究,并借宿在丹尼尔·伯努利的家中,与之一起工作。在这段时间里,欧拉一直专注于研究物理,而非医学。1733年,丹尼尔·伯努利无法忍受在科学院遭受到的种种麻烦与敌视,故回到瑞士在一学术岗位任职,当时年仅 26 岁的欧拉接替他成为了数学所所长。欧拉下定决心要尽量克服困难并安定下来,1734 年他结了婚并先后育有 13 个子女(仅有 5 个活到成年),欧拉非常享受孩子们在身边的生活,甚至一边抱着孩子,一边撰写论文,真是在任何情况下都能做研究的一位数学家!
在 18 世纪 30 年代期间,欧拉著作颇丰,他不仅在数论上取得了实质性的进展,在级数求和、力学领域也颇有成效。期间,他还担任俄国政府的科学顾问——为政府测绘地图,为俄罗斯海军提供建议,消防设备的设计审定,并为俄罗斯的学校编撰教科书。
欧拉终其一生致力于数论的研究。1729年12月,他收到了同事克里斯蒂安·哥德巴赫(Christian Goldbach)的来信,其最有名的就是尚未证实的哥德巴赫猜想。哥德巴赫在来信中提出了如下猜想:任何大于 2 的偶数都可写成两个质数之和。例如:
例如,当 时,我们分别得到质数 。那么所有这样形式的数都是质数吗?费马猜想它们都是,并宣称找到了一个生成质数的公式。但遗憾的是,欧拉在 1732年 就发现下一个数 是一个可以被 641 整除的十位数。自那以后,再无其它费马数被证明是质数,因此费马的这个猜想并不成立。
欧拉惊人的计算能力也是一个传奇。传说某天,欧拉的两个学生试图对一个复杂的收敛级数进行求和,但算到小数点后第 50 位上时两人的计算结果出现了分歧,欧拉只通过心算便得到了做出了正确地判断。欧拉诸如此类的惊人心算能力使法国数学家、物理学家弗朗索瓦·阿拉戈也不免为之惊呼:
“欧拉计算时显得毫不费力,就像人在呼吸或者鹰在风中保持平衡一样。”
欧拉面临的另一项挑战是找到四个不同的数字,使任意二者之和都等于一个完全平方数。而欧拉成功地找到了它们,分别是:18530,38114,45986 和 65570,比如下面几个示例:
在18世纪30年代,欧拉还研究无穷级数。例如,他对发散的调和级数产生了兴趣。
如果我们只看该级数的前 n 项,会发现它们的总和接近 ln(n)——实际上,正如欧拉所证,随着 n 变大,前 n 项之和与 ln(n) 的差越来越接近一个固定数,而这个奇妙的数如今被称为欧拉-马斯克若尼常数,它的值约为 0.5772…。但是我们对它的了解甚少,甚至不知道它是否是一个有理数。
另一个在当时难倒了许多数学家的问题是巴塞尔问题,即精确计算所有完全平方数的倒数的和。
欧拉早期的成就之一就是在他 28 岁(1735 年)就推导出了这个级数之和为 ,真正严密的证明在1741年发表。之后,他将计算推广到求所有 4 次方数,6 次方数…直至 26 次方数的倒数之和,这为后来的黎曼 函数奠定了基础。
接下来,让我们看一个欧拉在 1735 年解决的趣味谜题:哥尼斯堡七桥问题。中世纪城市哥尼斯堡由四个区域构成,通过七座桥相连,问题是:一个步行者怎样才能不重复、不遗漏地一次走完七座桥,最后回到出发点。欧拉将其转化为一个几何问题,通过对桥和陆地的连接点进行计数,证明了该走法不存在。
▌推荐观看视频《柯尼斯堡七桥问题是如何改变数学的》
戈特弗里德·莱布尼茨(Leibniz)就曾在 1679 年在给荷兰物理学家、数学家惠更斯(Christiaan Huygens)的信中提到,希望得到一种不涉及长度、距离和角度等度量概念的”位置分析”几何方法,而欧拉就是找到这样一种方法来解决“七桥问题”。现在,我们将其称为“拓扑学”或“橡皮几何学”——如果我们在橡皮上绘制地图并将其拉伸,就发生了类似的拓扑变换。
1736年,欧拉向维也纳宫廷天文学家乔凡尼·马里诺尼(Giovanni Marinoni)写了一封信,描述他对这个问题的看法:“虽然这个问题十分乏味,但在我看来,值得注意的是几何、代数甚至计数法都不足以解决这个问题。鉴于此,我想知道它是否属于曾让莱布尼茨兴趣盎然的位置几何学范畴。因此,经过认真思考,我得到了一种简单但完全成立的规则,借助该规则可以快速解决所有这类‘一笔画’问题。”
欧拉对哥尼斯堡七桥问题的解决方案被认为是对图论的最早贡献,如今,‘一笔画’问题已可以通过观察“节点”(代表陆地)和“边”(代表桥梁)构成的网络来解决了。但这并非由欧拉设计得到——用以表示这一谜题的网络直至150年后才真正诞生。
同年,欧拉发表了《力学》(Mechanica),这是他关于粒子动力学的第一篇论文。伴随着他对刚体运动——包括刚体自由运动和定点运动的深入研究,他于1750年在这一领域取得了最显著的成果。
通过选取一点作为坐标原点,选取相对于惯量的主轴坐标为体坐标轴系,欧拉推导出了我们现在所说的“欧拉运动方程”;转动惯量这个概念也来自欧拉。甚至在16年后,他还证明出刚体绕定点的任意有限转动等价于绕过定点某一轴的转动。这项工作大量地使用了微积分方程,这些方程的运用促进了微积分学的发展,而欧拉对此做出了很大贡献。
大约在 18 世纪 30 年代末期,欧拉右眼失明。尽管他将其归因于长期近距离进行地图学工作导致的劳累过度,但不排除眼部感染的可能性。即便如此,病痛并未影响欧拉的学术生产力:他继续撰写有关声学,音乐理论,造船,质数以及许多其它领域的论文。
▌在柏林时期
随着欧拉名声大噪,普鲁士腓特烈大帝在 1741 年邀请他加入恢复活力的柏林科学院担任数学部主任一职。欧拉考虑当时俄国的政治局势仍不稳定,就接受了这一邀请,并在随后在柏林渡过最多产 25 年时光。
起初,欧拉与腓特烈大帝相处融洽,甚至为他带来从自己花园里摘的草莓。但好景不长,特别是经过了德国和俄罗斯之间的七年战争之后,腓特烈大帝对科学院的运作越来越感兴趣,但他们之间的关系开始降温。
腓特烈大帝视自己为一个成熟有涵养、聪明非凡的人,欧拉在他的眼中就是一个乡下小子。欧拉发现了腓特烈的自命不凡,更不用提其狭隘和无礼了——腓特烈甚至称他为“我的独眼巨人”。传言说欧拉还曾因为其寡言受到了腓特烈的母亲(即普鲁士王太后)的询问,他回答倒也十分直白,“太后,我刚从那样一个国家(俄国)来,在那里你要是说多话,就会被吊死”。显然,王太后并不会被他的回复逗乐。
即便如此,欧拉仍恪尽职守、孜孜不倦地在各个领域探索,在 18 世纪 40 年代到 50 年代间,他完成了有关潮汐理论、月球运动、流体力学(河流运动)和弦振动的论文。
他当时最重要的著作是《无穷小分析引论》(Introductio in Analysin Infinitorum)。正是在此书中,他介绍了自己对数字 的一些早期研究成果:将 定义为阶乘倒数之无穷级数的和:
在引论中,欧拉将一些人们熟知的函数写作无穷级数的形式。他认为,任何一个函数(例如 )都可以展开为 的幂次数列。在当时,牛顿、莱布尼茨和其他数学家已经对以下展开式非常熟悉:
欧拉在此书中还留下了数学史上浓墨重彩的一笔。起初,三角函数正弦和余弦与指数函数 似乎并没有共同点,但如果我们引入复数 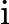 ,并对幂级数进行处理,便可以得到将它们联系起来的基本公式——欧拉公式:
这是一个将数学中最伟大的 5 个常数都包含在内的方程,后被物理学家理查德·费曼称为“欧拉的宝石”。
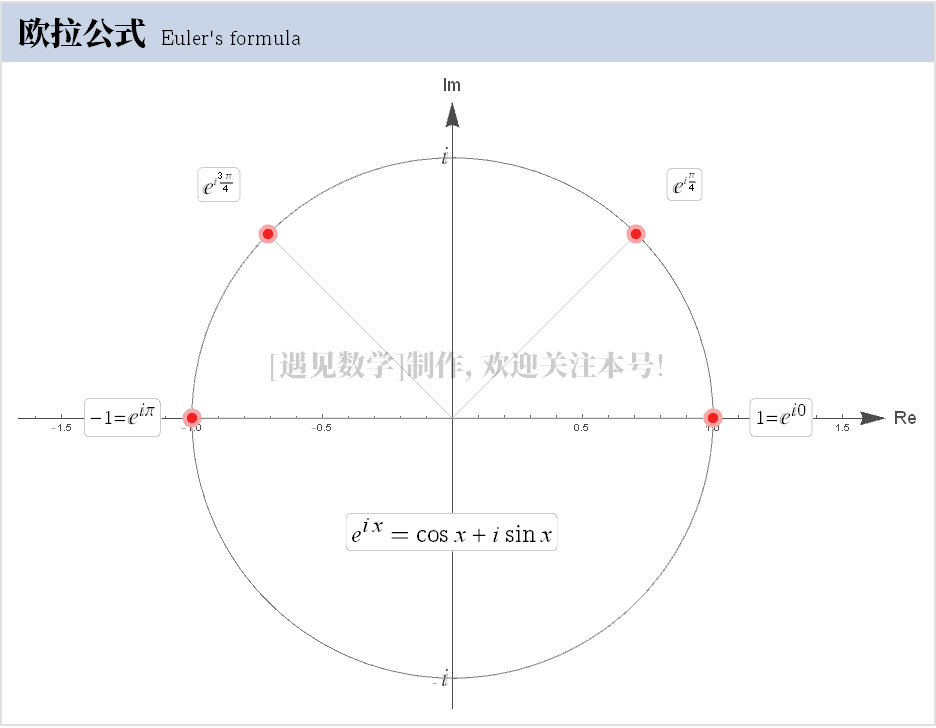
引论中还说到了许多有趣的事情。自笛卡尔提出将几何与代数相结合之后的百年间,数学研究方法逐渐从几何学过渡到代数学,并在当欧拉用代数方程,而不是圆锥截面,真正地定义了圆锥曲线(包括椭圆、抛物线和双曲线)时,代数学的应用达到了高潮。
他先向我们展示了这一等式: 接着说明了这条公式的几何含义:如果 是负数,我们将得到一个椭圆;如果 ,则会出现一条抛物线;如果 是正数,则是一条双曲线。然后,他将整个论证过程扩展到三维的二次曲面上,并对一共出现的 7 种情形进行代数研究,在此过程中他发现了双曲抛物面。
引论中另一个有趣的话题就是“整数分拆”(Integer partition)。如莱布尼茨致伯努利的信中所述,将一个正整数表示为若干个正整数的和共有几种方案?
令 表示无序拆分的方案个数——例如 ,对应于下面五种拆分方案: 。
由此,我们可以绘制一个数值表,但是如何得到 的划分数为3972999029388呢?
为了找到 的值,我们不如使用欧拉在引论中所用的五边形数定理,通过迭代得出 :
在引论中有所记载,关于“整数分拆”有一个奇妙的结论。当拆分成的数都是奇数时,例如在这样情况下,整数 9 有八种拆分方案:
当拆分成完全不同的数时,同样是 9,也恰好有八种拆分方案:
欧拉运用“母函数”(Generating function)证明,对于任何数字,拆分成的数都是奇数的方案数,等于拆分成完全不同的数的方案数,这是一个有趣且意想不到的结论。
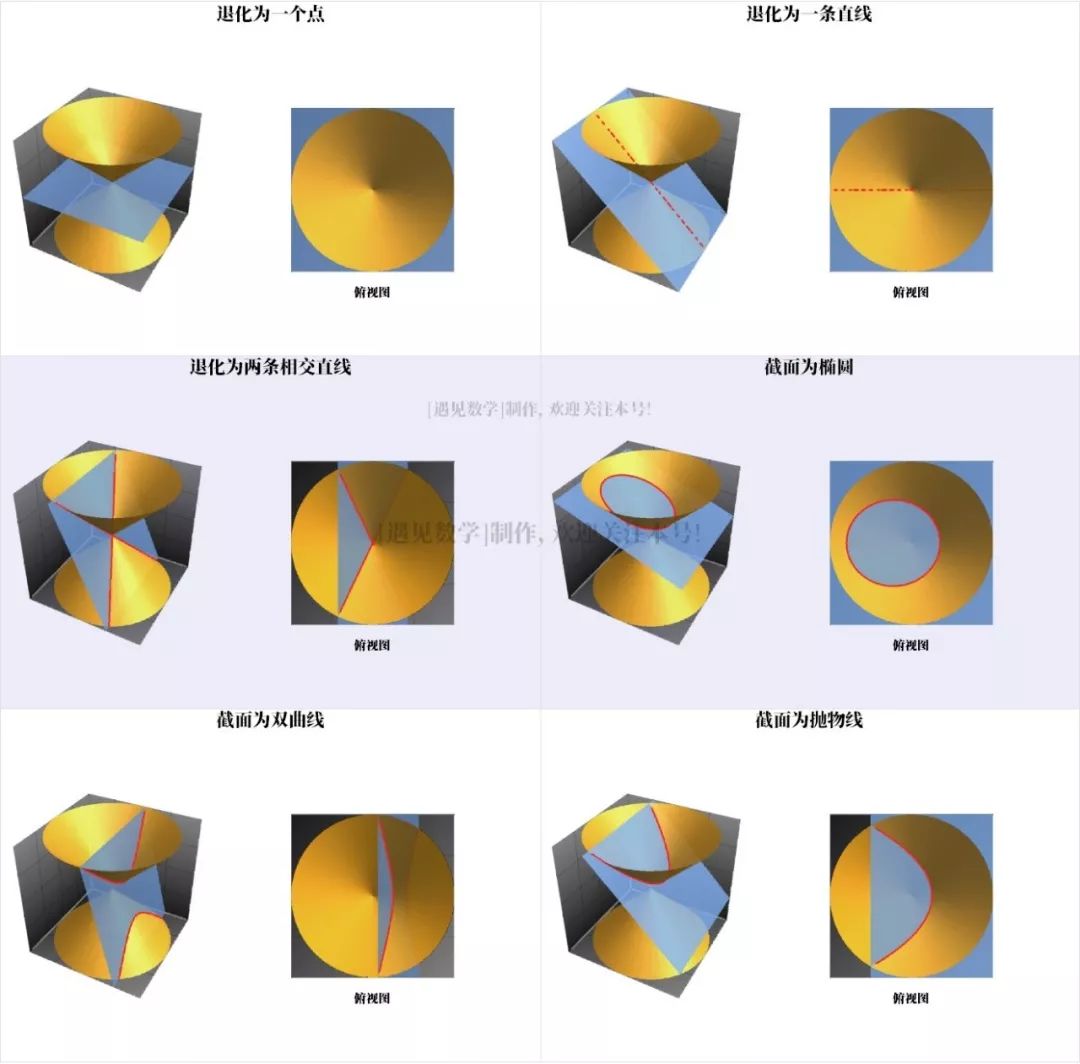
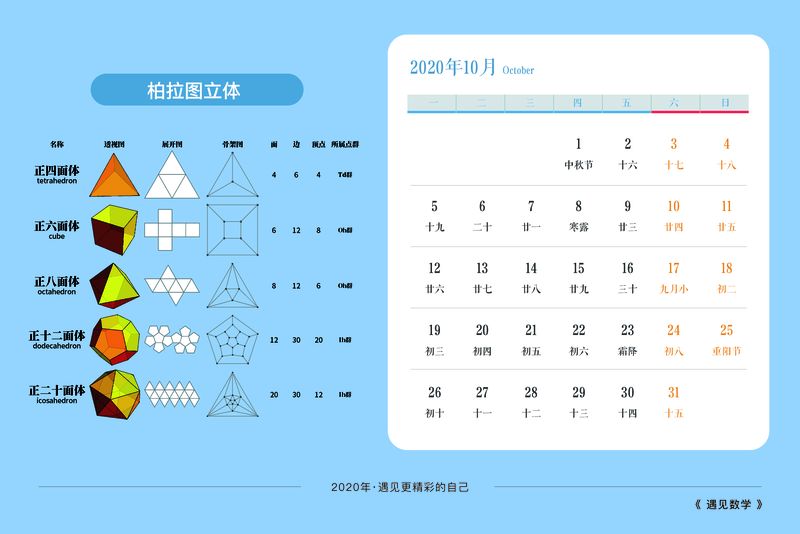
在欧拉于1750年致哥德巴赫的一封信中,他提及了当时的另一个研究领域。他一直在观察立方体及棱柱之类的简单多面体,并发现简单多面体的顶点数(V)、面数(F)、边数(E)之间始终存在一个关系式:
例如,上图的正六面体有 6 个面,8 个顶点和 12 条棱,则有 6 + 8 = 12 + 2,这一关系对于任何以平面为边界的实体都成立。这一定理曾被误认为是笛卡尔发现的,但后来人们并未找到笛卡尔为了推导出它使用的术语和动机:实际上,是欧拉引入了边的概念。但是,欧拉的证明不够完整——40年后,代数学家和数论学家勒让德(Legendre)给出了完整的证明。
欧拉最受欢迎的畅销书是《致一位德国公主的信》(Letters to a German Princess)。欧拉一直是一位思路清晰的写作者,这是当他应邀为安哈尔特·德绍公主函授基础科学课程时撰写的一系列杰作。这卷书囊括了200多封欧拉的书信,与科学相关的话题论及重力、天文学、光、声音、磁、逻辑学等方面。他写了为什么天空是蓝色的,为什么月亮升起时看起来更大,为什么山顶寒冷(甚至在热带地区也是如此),以及“人与动物的导电”等等。此书堪称有史以来最好的科普书之一。
▲ 1769年版《致一位德国公主的信》第一卷封面(图自维基)
1755年,欧拉完成了他在柏林创作的最后一本关于微积分学的巨著《微积分概论》。这本书包含了所有最新的研究成果,其中很多理论的诞生都要归功于欧拉。书中根据函数的基本概念介绍了微积分——毋庸置疑,正是欧拉引入了函数的记法 。除此之外,他还引入了 (求和符号),(-1的平方根)和 (自然对数的底数)等符号,尽管“”最初由威廉·琼斯(William Jones)于 1706 年提出,但却是经过欧拉的倡导才得以广泛流行。1768 年至 1770 年间,他在微分研究的基础上继续深入,发表了三册有关微积分的论文。
,并对幂级数进行处理,便可以得到将它们联系起来的基本公式——欧拉公式:
这是一个将数学中最伟大的 5 个常数都包含在内的方程,后被物理学家理查德·费曼称为“欧拉的宝石”。
引论中还说到了许多有趣的事情。自笛卡尔提出将几何与代数相结合之后的百年间,数学研究方法逐渐从几何学过渡到代数学,并在当欧拉用代数方程,而不是圆锥截面,真正地定义了圆锥曲线(包括椭圆、抛物线和双曲线)时,代数学的应用达到了高潮。
他先向我们展示了这一等式: 接着说明了这条公式的几何含义:如果 是负数,我们将得到一个椭圆;如果 ,则会出现一条抛物线;如果 是正数,则是一条双曲线。然后,他将整个论证过程扩展到三维的二次曲面上,并对一共出现的 7 种情形进行代数研究,在此过程中他发现了双曲抛物面。
引论中另一个有趣的话题就是“整数分拆”(Integer partition)。如莱布尼茨致伯努利的信中所述,将一个正整数表示为若干个正整数的和共有几种方案?
令 表示无序拆分的方案个数——例如 ,对应于下面五种拆分方案: 。
由此,我们可以绘制一个数值表,但是如何得到 的划分数为3972999029388呢?
为了找到 的值,我们不如使用欧拉在引论中所用的五边形数定理,通过迭代得出 :
在引论中有所记载,关于“整数分拆”有一个奇妙的结论。当拆分成的数都是奇数时,例如在这样情况下,整数 9 有八种拆分方案:
当拆分成完全不同的数时,同样是 9,也恰好有八种拆分方案:
欧拉运用“母函数”(Generating function)证明,对于任何数字,拆分成的数都是奇数的方案数,等于拆分成完全不同的数的方案数,这是一个有趣且意想不到的结论。
在欧拉于1750年致哥德巴赫的一封信中,他提及了当时的另一个研究领域。他一直在观察立方体及棱柱之类的简单多面体,并发现简单多面体的顶点数(V)、面数(F)、边数(E)之间始终存在一个关系式:
例如,上图的正六面体有 6 个面,8 个顶点和 12 条棱,则有 6 + 8 = 12 + 2,这一关系对于任何以平面为边界的实体都成立。这一定理曾被误认为是笛卡尔发现的,但后来人们并未找到笛卡尔为了推导出它使用的术语和动机:实际上,是欧拉引入了边的概念。但是,欧拉的证明不够完整——40年后,代数学家和数论学家勒让德(Legendre)给出了完整的证明。
欧拉最受欢迎的畅销书是《致一位德国公主的信》(Letters to a German Princess)。欧拉一直是一位思路清晰的写作者,这是当他应邀为安哈尔特·德绍公主函授基础科学课程时撰写的一系列杰作。这卷书囊括了200多封欧拉的书信,与科学相关的话题论及重力、天文学、光、声音、磁、逻辑学等方面。他写了为什么天空是蓝色的,为什么月亮升起时看起来更大,为什么山顶寒冷(甚至在热带地区也是如此),以及“人与动物的导电”等等。此书堪称有史以来最好的科普书之一。
▲ 1769年版《致一位德国公主的信》第一卷封面(图自维基)
1755年,欧拉完成了他在柏林创作的最后一本关于微积分学的巨著《微积分概论》。这本书包含了所有最新的研究成果,其中很多理论的诞生都要归功于欧拉。书中根据函数的基本概念介绍了微积分——毋庸置疑,正是欧拉引入了函数的记法 。除此之外,他还引入了 (求和符号),(-1的平方根)和 (自然对数的底数)等符号,尽管“”最初由威廉·琼斯(William Jones)于 1706 年提出,但却是经过欧拉的倡导才得以广泛流行。1768 年至 1770 年间,他在微分研究的基础上继续深入,发表了三册有关微积分的论文。
▌重返圣彼得堡
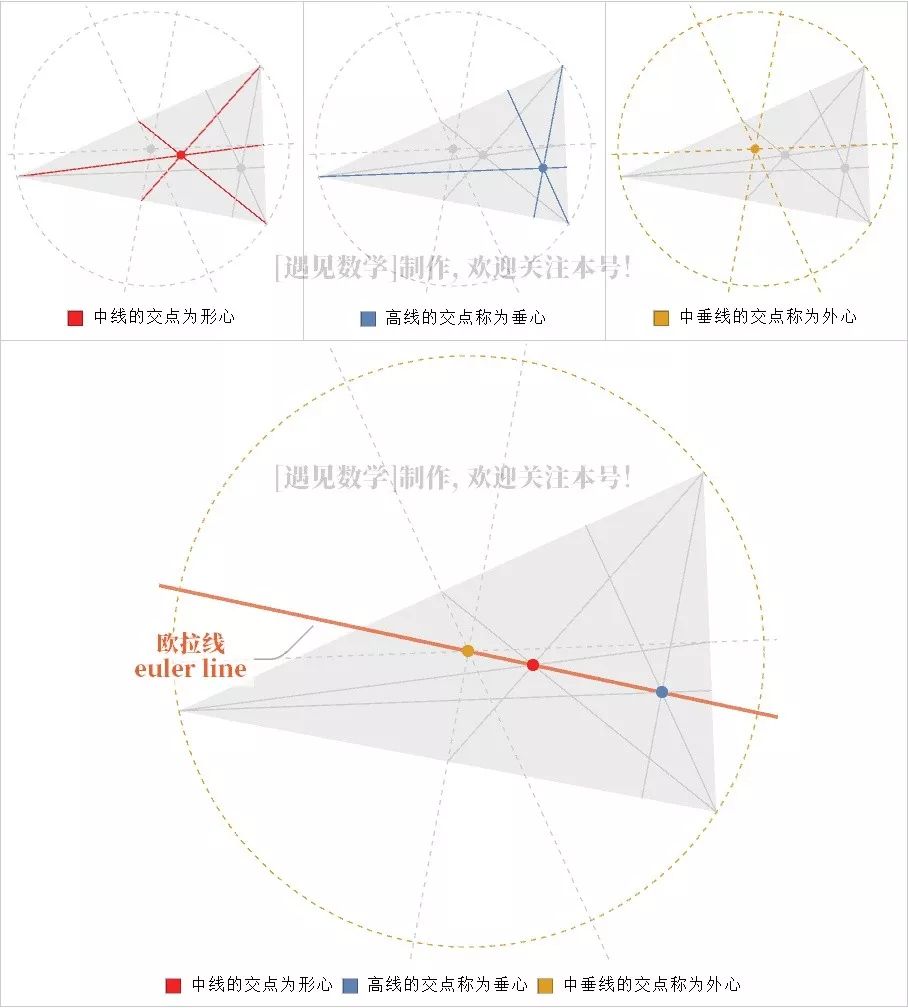
1766 年,59 岁的欧拉应叶卡捷琳娜二世之邀回到圣彼得堡,在经历了与腓特烈大帝相处的诸多不快后,这一邀请令他备感宽慰。多亏了开明的女皇,圣彼得堡的情况大有好转,欧拉在那里也得到了皇室规格的招待。他继续满怀热情地工作,很快就在纯粹几何学上获得了可喜的成果:在任意三角形中,都有三个特定点。第一个是垂心——从三角形的各个顶点向其对边所作的三条垂线的交点;第二个是重心——三角形的三条中线的交点;第三个是外心——三角形外接圆的圆心。通过坐标计算,欧拉证得了一个相当漂亮的结论:这三个点始终位于一条直线上(后人称之为三角形的欧拉线),并且重心恰好位于另外两点距离的三分之一处。
▲ 图左上表示从顶点到对边中点的三条线相交于形心;图左二表示从顶点到对边的三条垂线相交于垂心;图右上表示三角形的外接圆和外心;图下方表示三点位于一条直线,形心位于另外两点间距离的三分之一处。
欧拉对数论的兴趣一直延续到他的晚年,当时他对一些与费马相关的结论,特别是费马大定理进行了推论。
但费马在丢番图《算术》(Arithmetica)一书的页边空白处记录了如下猜想:对任意大于 2 的指数 n,不存在满足 的正数 。欧拉在其 1770 年发表的数论书中证明,两个立方数之和不可能等于另一个立方数( ),两个四次方数之和不可能等于另一个四次方数( )。费马大定理直到 1995 年才由英国数学家安德鲁·怀尔斯(Andrew John Wiles)得以彻底地证明。
欧拉与费马的另一联系是费马小定理,该定理指出,如果a是不能被给定质数 整除的任何整数,则 必能被 整除;例如,设 ,可推出 能被 29 整除。1760年,欧拉将这一结论扩展到质数以外的数字,引入欧拉 函数,证明了对于如果整数 和 互质, 总能被 整除。
数论中的又一结论涉及完全数(Perfect number,又称完美数、完备数),即一个数所有的真因子的和等于它本身。例如,6 是一个完全数,因为它的真因子是 1、2、3,它们的总和为 6;同样,28 也是一个完全数,因为它等于其真因子 1、2、4、7 和 14 的总和。
欧几里得在他的《几何原本》中证明,只要第二项 是质数,则形如 的每个数都是完全数。
此事实的充分性由欧几里得证明,而必要性则由欧拉所证明。
欧拉一生的最后几年虽然比他以往的生活更加安宁,但却充满了接踵而来的不幸。1771 年,欧拉的住宅被烧毁,书房化为灰烬,而他自己也差点丧命,但幸运的是,他的手稿得以保存了下来。没多久,他的爱妻去世,而他也再婚了。最终,欧拉几乎完全失明了——但当他在石板上奋笔疾书,他的两个儿子做笔录时,他表现出的生产力丝毫不减。
在 1725 年的一本趣味数学书中,法国数学家雅克·奥扎南(Jacques Ozanam)提出了排列 16 张宫廷牌,使每行每列都包含各种花色和各种数值及 J,Q,K,A 的方法,如下是几种排列方法。
用 25 张牌(包括 5 种花色和 5 种数值)也可以进行相似的排列。
那么,当牌数增加到 36 张时的排列呢?欧拉在他去世的前一年,在关于幻方(他的又一兴趣)的论文中,提出了“36 军官问题”(Thirty-six officers problem):
按方阵排列36名军官,由6个不同的军团各选6种不同军阶的6名军官组成,如何使得各行各列都有来自每种军阶的一名军官和来自每个军团的一名军官?
欧拉认为不存在符合要求的编排方法,而加斯顿·塔里(Gaston Tarry)在 1900 年左右通过列举所有的可能性终于证实了这一猜测。欧拉还称,对于任意军团数和军阶数(除该数为 4n+2,即 6,10,14,18…时),相应问题都存在解决方案。尽管欧拉方阵猜想直到 1960 年左右(即近 300 年后)才得到证明,但他的猜想只在该数为 6 时成立,其余情况都不成立。
欧拉直到生命的最后一刻还在孜孜不倦地工作。孔多塞侯爵的悼词将我们带回他的最后一个下午:1783年9月7日,他在一块石板上计算出气球上升定律后(后来这一新发现在整个欧洲引起了轰动),与莱克塞尔先生及其家人共进晚餐,谈论着赫歇尔行星(天王星)以及确定其轨道的计算。没过多久,他叫来了他的外孙,一边喝茶,一边与之玩耍,突然间,烟斗从他手中掉了下来,他停止了计算和呼吸。










![]()














![]()