在滕尚华（Shang-Hua Teng）的工作中，

理论与实践问题早已交织在一起。

现在他把注意力转向了非实用的事情。

（Emilio Flores供图）

滕尚华教授曾两次获得理论计算机科学的最高荣誉哥德尔奖（与Dan Spielman教授），

但他经常探索有趣的应用，

例如棋盘游戏。

对于滕尚华来说，理论计算机科学从来都不是纯粹的理论。

现年58岁的滕是南加州大学计算机科学教授，

曾两次获得哥德尔奖，该奖项旨在表彰突破性的理论工作。

但他经常努力以实用和有趣的方式将抽象理论与日常生活联系起来。

滕先生在文革前出生于中国北京，

他来到美国攻读研究生，

计划学习计算机体系结构，

但他很快就改变了方向，

专注于更抽象的数学理论。

他于1991年证明了一个关于如何最好地划分图的定理

[图，是由线（边）连接的点（节点）的网络]，

获得卡内基梅隆大学的博士学位。

虽然是理论性的，但这项工作有实际应用——

他发现，实际应用往往会带来新的理论见解。

在1993年美国宇航局NASA的暑期奖学金期间，

滕加入了一个使用“有限元”方法模拟流体动力学的团队，

该方法将复杂结构建模为许多小块的组合。

这些组合可以被视为图，

滕的任务是使他研究的划分方法适应这种新环境。

但他对NASA团队以前使用的划分技术感到好奇，

并开始与计算机科学家丹尼尔·斯皮尔曼

（Daniel Spielman，现在是耶鲁大学计算机科学教授）

一起研究其底层数学结构。

这个联合研究项目开启了长达数十年的合作，

为他们赢得了两项哥德尔奖。

这不是他唯一一次看到理论与实践之间的深刻联系。

“每一次，这些看似完全实用的东西背后，

都有这个美丽的数学。”滕说。

最近，滕将注意力转向了井字游戏、

国际象棋和围棋等游戏背后的美丽数学。

在这种“组合”游戏中，没有机会因素，

两个玩家总是对棋盘的状态了如指掌。

然而，组合博弈仍然具有挑战性，

因为博弈的玩法可能大得令人眼花缭乱。

博弈论研究人员喜欢将此类游戏推广到更大的棋盘上——

例如，井字游戏从 3×3 的方块放大到 n×n——

并量化在给定某个初始棋盘状态的情况下确定哪个玩家将获胜的难度。

不同的可能答案将游戏分类为相同的“复杂度类”，

这些类别在整个理论计算机科学中突然出现。

滕展示了一个数学定理如何激发了“一个美丽的棋盘游戏”的创造。

（Emilio Flores供图）

一个著名的复杂度类，有个平淡无奇的名字：P，

意思是“多项式时间”，

粗略地说，

它包含了可以在合理时间内解决的问题。

同样著名的NP类中的问题，

可能需要不合理的时间来解决，

但它们的解很容易检验。

对于另一个复杂度类（称为PSPACE）的问题，

即使是这种有效的验证也无法保证存在。

当研究人员考虑双人游戏的“深层逻辑”时——

“如果你做X，然后如果我做Y，然后如果你做Z”等等——

他们经常发现自己在谈论PSPACE。

但正如滕帮助证明的那样，

组合博弈的数学并不总是直截了当的。

复杂度类Wikipedia

量子杂志最近与滕进行了交谈，

讨论了他的计算机科学之路，

棋盘游戏背后的数学以及他父亲的影响。

为清楚起见，采访已经过压缩和编辑。

Q：在中国接受教育是什么感觉？

我出生在文革前，父亲是大学土木工程系主任。

革命发生时，他被囚禁在校园里。

然后整个校园都被送到了农村。

我曾经收集垃圾卖，

直到我几乎读完初中，

然后突然中国变了。

如果你学习好，

你可以进入大学，

我们没有其他机会找到任何固定的工作。

我醒了，

说：“我需要学习。”

Q：您是如何选择计算机科学的？

我想在高中毕业后学习生物学。

我不知道为什么，

但我父亲对此不是很满意。

我的数学成绩不错，

他问我是否想做数学。

我说没有。

然后他说，“你知道，

有一门新学科叫计算机科学，

它真的很好。”

不知何故，

他促使我主修计算机科学。

当时的教育非常基础。

我们没有接触过大多数东西，

计算机科学甚至不是一个部门；

而是电气工程专业。

但完全是偶然的，

我们被训练成微积分的数学学生，

我学到了一些东西，

最终对成为一名理论家很有用。

如果没有它，我可能没有机会通过。

如今，孩子们更有天赋：

从高中开始，他们是比我来到这个国家时更有天赋的数学家。

滕在南加州大学校园内（Emilio Flores供图）

Q：这些知识差距如何影响你的研究生经历？

有一天我的导师Gary Miller加里·米勒

发现我从未听说过NP。

这是在某次讨论中。

他说，“这个问题看起来很难”。

我说：“嗯”。

他说：“你不相信我？”

然后他开始证明这一点，

中途他猛地转向我，

因为我只是坐在那里，

他说，“你知道什么是NP困难吗？”

我说不知道。

我以为那是我和他一起工作的最后一天，

但他继续告诉我（关于NP难度的）定义。

他说：“不知道没关系，只要你能思考就行”。

他对我产生了巨大的影响。

Q：你主要是一名理论家，但在你的整个职业生涯中，

你都涉足了工业领域。

这项实际工作如何与您的理论研究联系起来？

在我的论文中，我开发了一些用于划分图的几何方法。

我能够证明，

这一系列几何方法为有限元图提供了可证明的良好切割。

在导师的推荐下，我开始在美国宇航局和波音航空航天公司发表演讲。

在波音公司，我记得其中一个机翼的3D模型已经有近一百万个元件，

他们甚至无法将其加载到一台机器中。

因此，他们希望将这张图切割成不同的组件，

将它们放在具有相似计算负载的不同机器上，

并最大限度地减少通信。

这就是为什么在数学上那是一个图切割的公式。

在理论计算机科学中，

即使问题的外观发生巨大变化，

从最优化到博弈论，

基本的数学原理也经常保持不变。

当你做研究时，

感觉不像是一个剧烈的变化。

Q：说到博弈论，我看到你帮助设计了一个棋盘游戏。

这是怎么发生的？

哦，我喜欢棋盘游戏！

与复杂性理论有着美好的联系。

但大多数情况下，我是我学生的学生。

我在波士顿大学做一个演讲，

讲一个漂亮的离散定理，

叫做斯佩纳引理（Sperner’s lemma）。

这在一个维度上非常简单。

有一条线段，其中一端为红色，一端为蓝色。

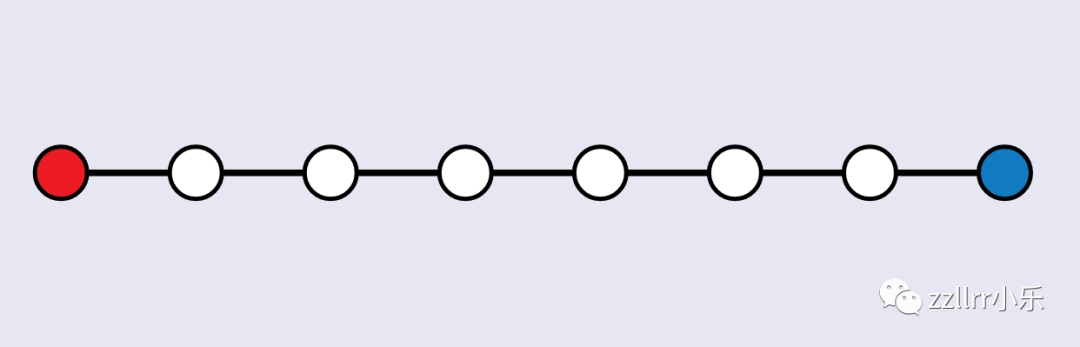
可以将其划分为子线段[两端都有节点]，

并将每个新节点着色为红色或蓝色。

然后[无论你如何给它们着色]我们知道，

一定有一条线段同时具有两种颜色。

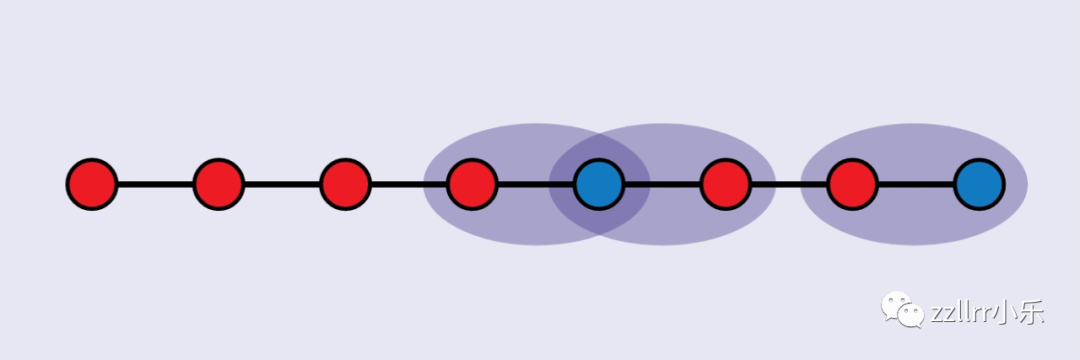
在二维空间中，它非常迷人。

有一个三角形，现在有三种颜色：

一个角是红色的，一个是蓝色的，一个是绿色的。

将此三角形划分为较小的三角形，

以便将边分成几段。

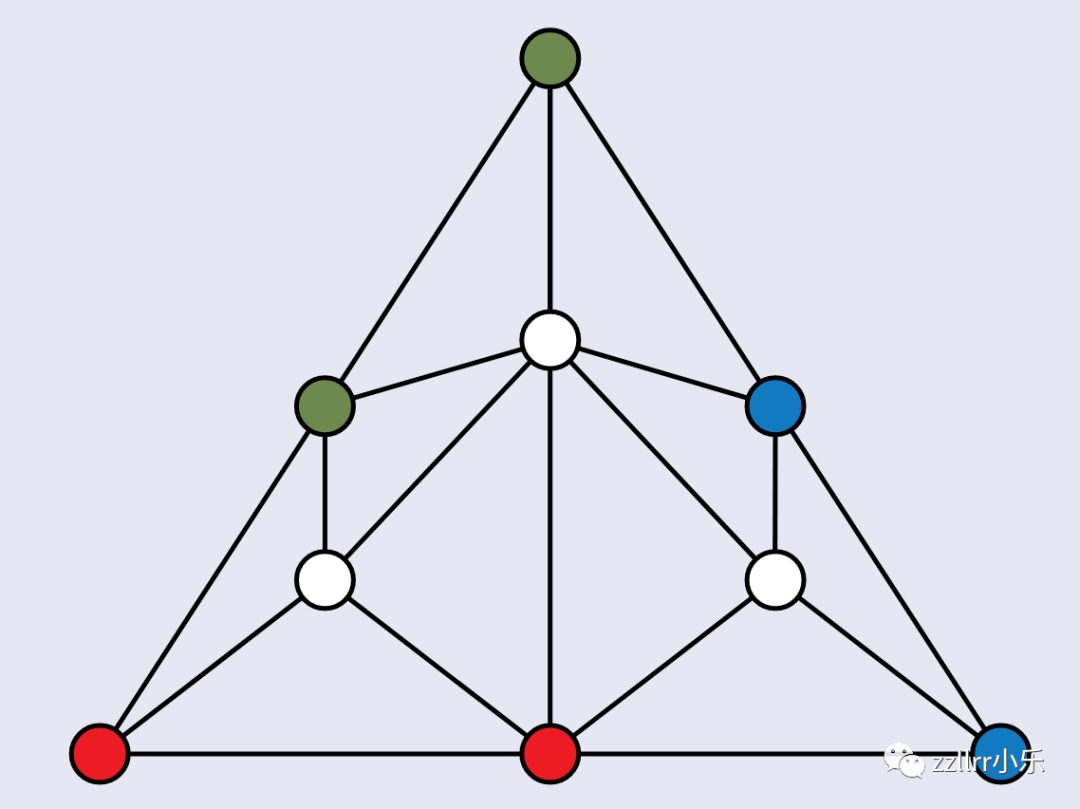
每条外部的边都遵循一维规则：

节点只能使用线段最两端的颜色之一。

而在三角形内部，

您可以按照自己喜欢的任何方式选用所有三种颜色。

斯珀纳引理说，无论你用什么方式划分它，

如果你做这种着色，

一定有一个三角形具有所有三种颜色。

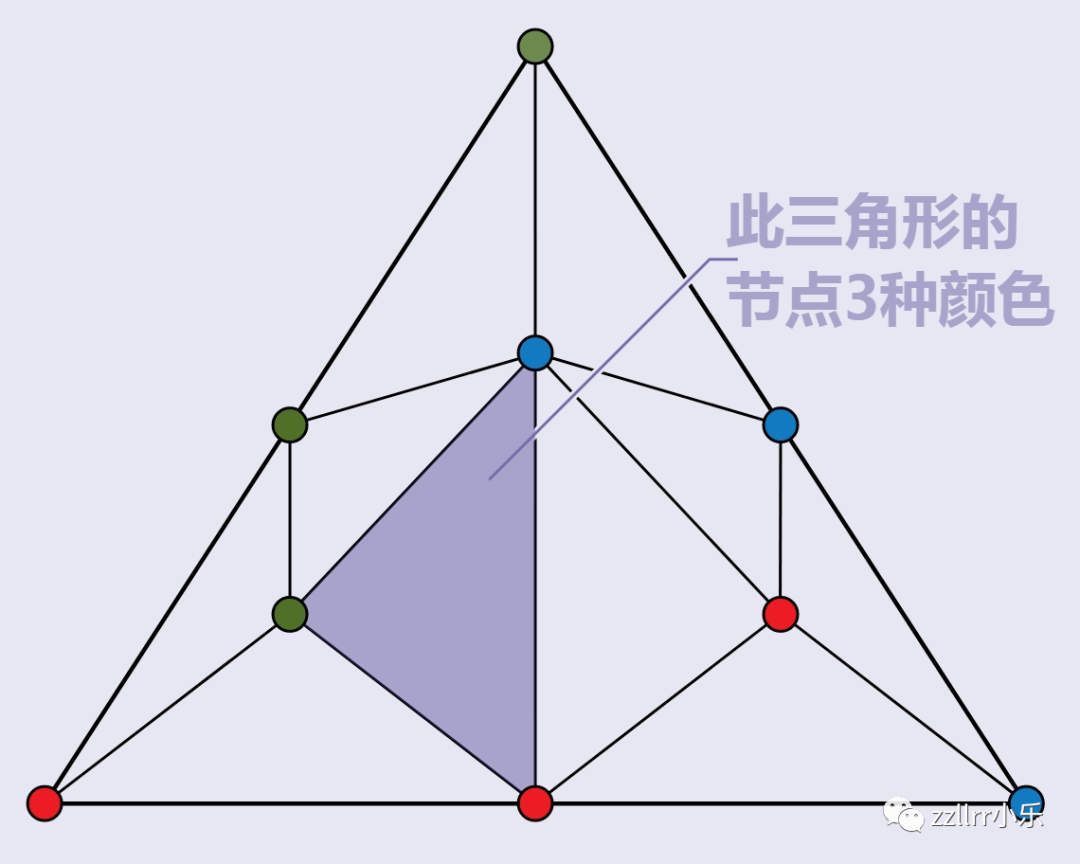
凯尔·伯克（Kyle Burke）是我的学生，

当时从事数值分析工作。

他来到我的办公室，

说可能会有一个漂亮的斯佩纳引理棋盘游戏：

两个玩家迭代地给一个棋盘上色，

谁产生出一个三色三角形，谁就会输掉游戏。

最好的棋盘游戏有赢家而不是平局，

在这里，显然有人会赢。

为什么？

因为斯佩纳引理！

我打电话给我的朋友大卫·埃普斯坦

（David Eppstein，加州大学欧文分校Irvine），

来谈谈什么是好的棋盘游戏。

他说：“一个好的游戏有简单的规则和漂亮的棋盘，

而且它必须是PSPACE难度的。”

因为如果你能在多项式时间内解决它，

计算机就会一直打败你。

所以我们通过了这些标准。

凯尔说：“这个游戏简单吗？”

我说：“是的，就是一句话！”

他说：“这个游戏是丰富多彩的吗？”

我说：“设计使然！”

然后他说，

“如果我证明这是PSPACE困难的，

我能获得博士学位吗？”

我答应了，他照做了。

他的定理有许多不同的方面。

它揭示了关于不动点的某些事情，

这是数学中一个非常美丽的概念。

滕与前学生凯尔·伯克（左）和现任研究生马修·费兰德（中）;

三人最近发表了一篇关于博弈求和的论文。（图片由滕尚华提供）

Q：我可以在任何地方玩游戏吗？

它在网上可用（有一些微调）。

Q：你喜欢玩什么游戏？

我是博弈理论家。[笑]。

我和女儿一起玩了一点，

但我不是从小玩这些长大的。

不像我的学生那样，他们一生都在玩游戏。

Q：你在棋盘游戏的数学方面还做了哪些工作？

我们最近有一篇关于一个悬而未决问题的论文：

如果你把两个多项式时间可解的游戏并排放置在一起，

这会使它们成为PSPACE困难吗？

在每一步中，你只能玩其中之一。

这称为博弈求和（summation of games）。

Q：将两个游戏放在一起意味着什么？

在古代围棋游戏中，当你放下足够多的石头棋子时，

你会得到许多独立的竞技场，

所以从某种意义上说，

你是在玩一把游戏。

你必须担心这个角落和那个角落。

你想赢得整个部分，

但这并不意味着你必须赢得每一个部分。

这在哲学上很有趣，对吧？

这就像你有一场战争，它有很多战斗，

但你的注意力是有限的。

在任何时候，你只能在其中一个战场上做出一个决定，

而你的对手可以在其他战场上做出反应或加倍努力。

我试图向父亲解释这一点。

当你玩一把游戏时，

它实际上意味着：你如何在战略上输掉？

我们在两个游戏中证明了它，

但是你可以把三个游戏放在一起，

这个定理仍然是正确的：

三个多项式时间游戏放在一起可以变成PSPACE困难的。

滕在棋盘游戏的数学中找到了更广泛的经验教训。

“当你玩一盘游戏时，它实际上意味着：你如何在战略上输掉？”

（Emilio Flores供图）

Q：自从他把你推向计算机科学以来，你父亲对你多年来所做的不同工作有何反应？

他经常问我：“你为什么要这样做？”

理论上的工作，往往多年没有结果，

他逐渐明白了这一点。

早期我可以谈论有限元方法——

他们也在土木工程中教授这种方法。

但是我不知道如何谈论这个娱乐数学。

然后我想到了中国著名小说《三国演义》中的成语。

其中一个人物，诸葛亮，几乎是一个完美的战略家，

成语说：“三个臭皮匠，顶个诸葛亮”。

以这种轻松的方式来说，

三个普通人加在一起就可以完美。

但纵观这个成语的历史，不同地区的发音不同，

“皮匠”与“裨将”的发音相同。

所以它说，

“三个裨将加在一起比这个完美的战略家要好”。

我对父亲说，这正是我们用博弈求和证明的定理。

裨将代表[解决]多项式时间博弈的算法：

在每个战场上，他们知道如何获胜。

但困难的部分是知道什么时候输，

而不是如何赢得每场比赛。

如果有人能玩这种艰难的游戏，

他们真的是最好的战略家。

裨将不会做出这些深刻的逻辑决策，

但不知何故，

如果你把它们很好地放在一起，

他们并不比这个完美的战略家差。

我告诉我爸爸，

“我终于意识到这个数学定理相当于我们著名的成语之一！”

当时他已经94岁了，他非常尖刻地说：

“这是一个好的尝试。”

我不太能说服他。

那是我与他的最后一次技术对话；

几个月后，他去世了。

每当我想解释我的工作时，

这是我的亮点部分。