
编译 | 杏花
编辑 | 青暮
在机器学习领域,人工神经网络逐年扩大规模,并取得了巨大成功,但同时它也制造了一个概念性难题。
当一个名为 AlexNet网络在2012年赢得年度图像识别比赛时,大约有6,000万个参数。这些参数在训练过程中进行了微调,使AlexNet能够识别出以前从未见过的图像。两年后,一个名为 VGG 的网络以超过 1.3 亿个参数赢得了全场喝彩。如今,一些人工神经网络(或ANN)甚至达到了数十亿个参数。
这些庞大的网络,在图像分类、语音识别和文本翻译等任务上取得了惊人的表现,已经开始主导机器学习和人工智能领域。然而,这些网络仍然是神秘的,其惊人的力量背后的原因仍然难以捉摸。
但一些研究人员表明,这些强大网络的理想化版本(比如无限宽)在数学上等同于更古老、更简单的机器学习模型,即内核机(kernel machines)。如果这种等价性可以扩展到理想化的神经网络之外,就可以解释实际的人工神经网络为何能取得惊人的效果。
人工神经网络的一部分神秘之处在于,它们似乎颠覆了传统的机器学习理论,而这些理论严重依赖统计学和概率论的观点。在通常的思维方式中,机器学习模型,包括神经网络,通过学习样本数据中的模式来预测新数据——特别是当它们拥有正确数量的参数时,表现最佳。
如果参数太少,学习模型可能会过于简单,无法捕捉训练数据的所有细微差别。若参数太多,模型则会变得过于复杂,在训练数据中学习模式的粒度太细,以至于在要求对新数据进行分类时无法泛化,这种现象称为过拟合。“这是在以某种方式很好地拟合数据和根本不拟合之间的平衡,我们需要找到一个居中点。”加州大学圣地亚哥分校(University of California, San Diego)机器学习研究员Mikhail Belkin如是说。

众所周知,像VGG这样的深度神经网络参数太多,应该会过拟合,但事实并非如此。而且恰恰相反,这类网络对新数据的泛化能力惊人的好——直到最近,还没人知道其中的原因。
这并不是因为缺乏这方面的探索。例如,于今年8月去世的耶路撒冷希伯来大学计算机科学家和神经科学家Naftali Tishby认为,深度神经网络首先拟合训练数据,然后(通过信息瓶颈)丢弃无关信息,这有助于它们泛化。但其他人认为,这并不适用于所有类型的深度神经网络,这个想法仍然存在争议。
现在,内核机和理想化神经网络的数学等价性为这些过度参数化的网络效果如此好的原因和过程提供了线索。内核机是一种算法,它通过将数据投射到极高的维度中来寻找数据中的模式。也就是说,通过研究理想化神经网络在数学上易于处理的内核机等价对应物,研究人员正在了解为什么深度网络尽管具有令人震惊的复杂性,但在训练过程中会收敛到可以很好地泛化到未见过的数据的解决方案。
“神经网络有点像Rube Goldberg机器。你不知道其中哪一部分真正重要。” Belkin说。“我认为将[它们]简化为内核方法(因为内核方法没有这么复杂),在某种程度上允许我们打开这个黑箱。”
内核方法或内核机,依赖于具有悠久历史的数学领域。这要追溯到19世纪德国数学家卡尔·弗里德里希·高斯(Carl Friedrich Gauss),他提出了同名的高斯核函数,这一函数将变量x映射到一个熟悉的钟形曲线的函数。20世纪初,英国数学家James Mercer用核函数来解积分方程,核函数的现代用法开始兴起。到了20世纪60年代,核函数被用于机器学习,以处理不适合简单分类技术的数据。
理解内核方法需要从机器学习中被称为线性分类器的算法开始。假设猫和狗只能使用二维数据进行分类,这意味着你需要两个特征(比如鼻子的大小,我们可以在 x 轴上绘制,而耳朵的大小可以在y轴上表示)来区分两种类型的动物。根据x-y平面上绘制标记的数据,猫应该在一个集群中,而狗在另一个集群。
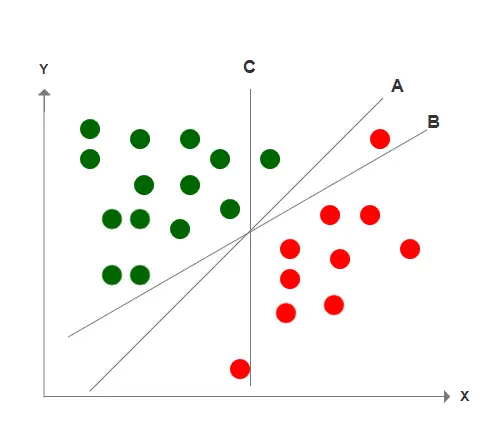
然后我们可以使用标记的数据训练线性分类器,找出一条将两个集群分开的直线。这涉及找到表示线的方程的系数。现在,给定新的未标记数据,通过看这些数据落在线的哪一侧,很容易将其归类为狗或猫。
然而,爱狗人士和爱猫人士会对这种过于简单化的做法感到震惊。许多类型的猫和狗的鼻子和耳朵的实际数据几乎肯定不能被线性分隔符分割。在这种情况下,当数据是线性不可分的,可以将其转换或投影到更高维的空间中。(一种简单的方法是将两个特征的值相乘,从而创建出第三个特征:也许将狗与猫区分开来的鼻子和耳朵的大小之间存在某种相关性。)
更普遍地说,在高维空间中查看数据更容易找到线性分隔符,当空间具有三个以上的维度时,该线性分隔符被称为超平面。当这个超平面被投影回较低维度时,它将呈现出带有曲线和摆动的非线性函数的形状,将原始低维数据分成两个集群。
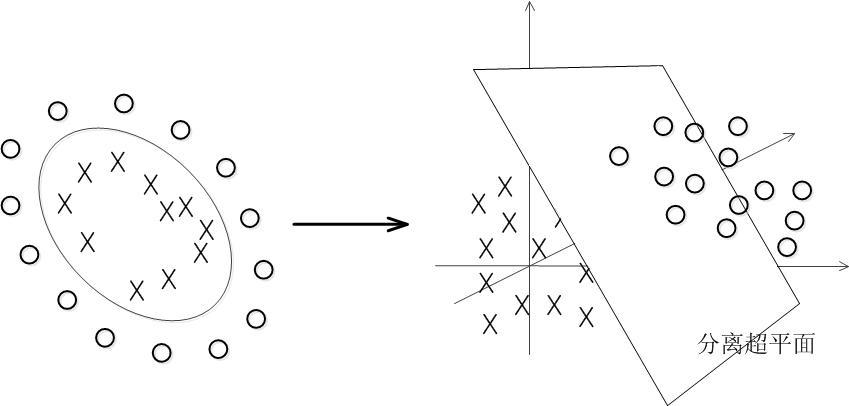
然而,当我们处理真实数据时,在高维中找到超平面的系数通常是计算效率低下的,有时甚至是不可能找到的。但内核机不存在这种情况。
内核机的强大之处在于它们能完成这两件事。首先,内核机将低维数据集中的每个点映射到更高维数据集中的一个点。这个超空间的维度可能是无限的,取决于映射,这可能会带来一个问题:找到分离超平面的系数涉及到计算每一对高维特征的内积,当数据被投射到无限维时,这就变得很困难。
其次,给定两个低维数据点,内核机可以使用核函数输出一个数字,这个数字等于相应的高维特征的内积。关键是,该算法可以使用这种技巧来找到超平面的系数,而无需真正进入高维空间。
加州大学伯克利分校名誉教授Bernhard Boser说,“内核技巧的伟大之处在于,所有计算都发生在低维空间”,而不是可能的无限维空间。
Boser和他的同事Isabelle Guyon以及Vladimir Vapnik在20世纪80年代末和90年代初发明了一类称为支持向量机 (SVM) 的内核机,当时他们都在新泽西州霍尔姆德尔的贝尔实验室(Bell Labs)。虽然从20世纪60年代开始,各种类型的内核机已经在机器学习领域取得了显著的成就,但正是随着SVM的发明,它们才登上了舞台的中心。事实证明,SVM 非常强大。到21世纪初,它们被广泛应用于生物信息学(例如,用于发现不同蛋白质序列之间的相似性并预测蛋白质的功能)、机器视觉和手写识别等领域。
SVM继续主导机器学习领域,直到 2012 年AlexNet 的到来,标志着深度神经网络发展成熟。随着机器学习社区转向ANN,SVM陷入困境,但它们(以及一般的内核机)仍然是强大的模型,有很多东西值得我们学习。例如,他们可以做的不仅仅是使用内核技巧来找到一个分离超平面。
“如果你有一个强大的内核,那么你就可以将数据映射到一个无限维且非常强大的内核空间,”谷歌研究大脑团队的研究科学家张志远(Chiyuan Zhang)说道。“在这个强大的隐藏空间中,你总能找到一个线性分隔符来分隔数据,而且有无限多种可能的解决方案。”
但是,内核理论不是让你仅仅选择一个任意的线性分隔符,而是通过限制搜索的解决方案的空间,选择一个可能的最佳分隔符(对于某些“最佳”的定义而言)。类似于减少模型中的参数数量以防止其过拟合,这一过程称为正则化。张志远想知道深度神经网络是否也在做类似的事情。
深度神经网络由多层人工神经元组成。它们有一个输入层、一个输出层和至少一个夹在它们之间的隐藏层。隐藏层越多,网络就越深。网络的参数代表了这些神经元之间连接的强度。例如,训练一个网络进行图像识别,需要反复向它展示之前分类过的图像,并确定其参数值,以帮助它正确地描述这些图像。经过训练后,神经网络成为了一个将输入(比如图像)转换为输出(标签或类别)的模型。
2017年,张志远和同事对AlexNet和VGG等网络进行了一系列实证测试,以查看用于训练这些ANN的算法是否以某种方式有效地减少了可调参数的数量,从而产生了一种隐式正则化形式。换句话说,训练机制是否使这些网络无法过拟合?
张志远团队发现事实并非如此。使用巧妙操纵的数据集,张教授的团队证明了AlexNet和其他类似的人工神经网络确实会过拟合,而不是泛化。但是,当给定未更改的数据时,使用相同算法训练的相同网络并没有过拟合——相反,它们泛化得很好。这种隐式正则化不可能是答案。张志远说,这一发现要求“更好地解释描述深度神经网络中的泛化特征”。
与此同时,研究表明,较宽的神经网络在泛化方面通常与较窄的神经网络表现一样好,甚至更好。对某些人来说,这暗示着或许可以通过采用物理学中的策略来理解人工神经网络,“研究极限情况有时可以简化问题。”谷歌研究大脑团队的研究科学家Yasaman Bahri说。为了解决这种情况,物理学家经常通过考虑极端情况来简化问题。例如,当系统中的粒子数趋于无穷时会发生什么?Bahri说:“在这些限制条件下,统计效应会变得更容易处理。”从数学上讲,如果神经网络层的宽度——即单层神经元的数量——是无限的,那么神经网络会发生什么?
1994年,现为多伦多大学名誉教授的Radford Neal提出了一个关于具有单个隐藏层的无限宽网络的确切问题。他指出,如果这个网络的权重被重新设置或初始化,具有某些统计性质,那么在初始化时(在任何训练之前),这样的网络在数学上等价于一个众所周知的核函数,称为高斯过程。20多年后,在2017年,包括Bahri在内的两个研究小组表明,具有许多隐藏层的无限宽理想化深度神经网络也是如此。
这背后的含义是惊人的。通常情况下,即使在训练了深度网络之后,也不能使用解析数学表达式来对未见过的数据进行预测。你只需要运行深度网络,看看它说了什么——它就像一个黑匣子。但在理想化的场景中,初始化时网络等价于高斯过程。这时你可以抛弃神经网络,只训练有数学表达式的内核机器。
“一旦你把它映射到高斯过程中……你就可以通过分析计算预测应该是什么,”Bahri说。
这已经是个里程碑式的发现,但它并没有从数学上描述在实践中最常见的训练形式所发生的情况。在后一种情况下,尚不清楚该解决方案如何能够很好地泛化。
部分谜团集中在如何训练深度神经网络上,这涉及一种称为梯度下降的算法。“下降”一词指的是,在训练过程中,网络穿越了一个复杂的、高维的、布满山丘和山谷的景观,景观中的每个位置都代表了网络对给定的一组参数值所造成的误差。最终,一旦参数得到适当调整,人工神经网络就会到达一个称为全局最小值的区域,这意味着它将尽可能准确地对训练数据进行分类。训练网络本质上是一个优化问题,即寻找全局最小值,训练后的网络表示将输入映射到输出的几乎最优函数。这是一个难以分析的复杂过程。
西雅图华盛顿大学的机器学习专家Simon Du说:“如果你应用一些广泛使用的算法,如梯度下降,(人工神经网络)可以收敛到全局最小值,现有的理论无法保证这一点。” 到2018年底,我们开始明白其中的原因。
同样,正如重大科学进步常表现的那样,基于对无限宽网络的数学分析,以及它们与更容易理解的内核机器之间的关系,多个研究小组同时得出了一个可能的答案。在Simon Du的团队和其他人发表论文的时候,一位名叫Arthur Jacot的年轻瑞士研究生在该领域的旗舰会议NeurIPS 2018上展示了他的团队的成果。
虽然各团队在细节和工作框架上有所不同,但本质是一致的,即无限宽的深度神经网络,其权值是根据特定的统计属性初始化的,不仅在初始化时,而且在整个训练过程中都与核函数完全相同。关于权重的一个关键假设是,它们在训练过程中单个变化很小(尽管无限数量的小变化的净影响是显着的)。Jacot和他在瑞士洛桑联邦理工学院的同事证明了一个无限宽的深度神经网络总是等同于一个在训练期间不会改变的内核,它甚至不依赖于训练数据。核函数只依赖于神经网络的结构,如连接的深度和类型。基于它的一些几何特性,该团队将其内核命名为神经正切核。
“我们知道,至少在某些情况下,神经网络可以像内核方法一样运行,”雅科特说。“这是尝试真正比较这些方法以试图了解差异的第一步。”
这个结果最重要的发现是,它解释了为什么深度神经网络,至少在这种理想情况下,会收敛到一个好的解。当我们在参数空间中查看人工神经网络时,即从其参数和复杂的损失景观来看,这种收敛性很难在数学上证明。但由于理想的深度网络相当于一个内核机,我们可以使用训练数据来训练深度网络或内核机,最终都会找到一个近似最优的函数,将输入转换为输出。
在训练过程中,无限宽神经网络所代表的函数的演化与内核机所代表的函数的演化相匹配。当我们看到函数空间时,神经网络和它的等效内核机都在某个超维空间中滚下一个简单的碗状景观。很容易证明梯度下降会让你到达碗的底部——全局最小值。至少对于这种理想化的场景,“你可以证明全局收敛,”Du说。“这就是为什么学习理论社区的人们这么兴奋。”
并不是每个人都相信核函数和神经网络之间的这种等价性适用于实际的神经网络——这些神经网络的宽度是有限的,并且其参数在训练过程中会发生巨大变化。“我认为还需要把一些地方联系起来,”张志远说。此外,还有心理方面的原因:神经网络本身就很神秘,将它们简化为内核机让张感到失望。“我有点希望这不是最终答案,因为从旧理论可用的意义上来说,它会让事情变得不那么有趣。”
但其他人却很兴奋。例如,Belkin认为,即使内核方法是旧理论,它们仍然没有被完全理解。他的团队根据经验表明,内核方法不会过拟合,并且在不需要任何正则化的情况下可以很好地泛化到测试数据,这与神经网络类似,且与我们对传统学习理论的预期相反。“如果我们了解了内核方法的发展,那么我认为这确实为我们提供了打开神经网络这个神秘盒子的钥匙,”Belkin如是说。
研究人员不仅对核函数有更牢固的数学掌握,从而更容易将它们作为模拟物来理解神经网络,而且从经验上讲,核函数也比神经网络更容易使用。核函数远没有那么复杂,它们不需要随机初始化参数,而且它们的性能更具有可重复性。研究人员已经开始研究现实网络和核函数之间的联系,并对他们在这一新理解上能走多远感到兴奋。
“如果我们建立了绝对、完全的等价,那么我认为它将在某种程度上改变整个游戏。”Belkin说。
![]()

